Chapter 4 Modeling canine rabies virus transmission dynamics
This chapter was originally published in:
Rajeev M., Metcalf C.J.E., & Hampson K. Modeling canine rabies virus transmission dynamics. Chapter in Rabies, 4th Edition. May 2020.
The authors’ pre-editorial version is included here.
Abstract
Mathematical models of infectious disease are used to develop an understanding of disease dynamics and aid in designing control strategies. Modeling can also shed light on how dynamics, and therefore intervention strategies, may change as control is implemented. In light of the mounting evidence that elimination of canine rabies is a realistic objective, the WHO has set a global target of zero human deaths due to dog-mediated rabies by 2030. In this chapter, we focus on how dynamic epidemiological modeling can guide efforts to achieve this goal. We review existing modeling work and identify insights generated, outstanding questions, and gaps in our knowledge. We further discuss the role that modeling can play in the future to inform elimination.
Key Words: Canine rabies, Zero by 30, disease modeling, mass dog vaccination, transmission dynamics
4.1 Introduction
Models of disease dynamics are a powerful tool in the arsenal of disease prevention and control efforts, and can be used to estimate key epidemiological parameters, establish targets for control, and guide policy [1]. Modeling can also identify counter-intuitive outcomes that emerge as interventions are implemented, and challenges in the endgame when disproportionate resources are necessary to reach the last mile of elimination [2]. In light of the global goal to eliminate human deaths due to dog-mediated rabies by 2030, models of rabies virus transmission have potential to inform control efforts as countries progress towards elimination.
4.1.1 History of modeling rabies virus transmission dynamics
Modeling rabies in domestic dog populations is a relatively nascent effort. In contrast, models of wildlife rabies guided early control efforts [3]. Elimination of fox rabies in Europe was kick-started by modeling studies that demonstrated the feasibility of control [4]. Surveillance of rabies in wildlife systems in Europe and North America provided rich data sets to characterize dynamics, identifying the wave front of outbreaks to target control geographically [5], establishing that landscape features such as rivers act as barriers to disease dispersal [6], and delineating how birth pulses shape seasonality in transmission [7]. This work provides a foundation for modeling canine rabies, but there are fundamental differences between wildlife and domestic dog systems. Human populations, behavior, and culture structure dog populations [8]. In addition, canine rabies persists in low- and middle-income countries where surveillance capacity is limited and representative disease data are lacking [9]. Beyond capturing core infection biology, models of canine rabies must also encompass human influences and be tractable to interpretation in data-sparse settings.
4.1.2 The modeling backbone for canine rabies
Rabies can be modeled in an SEIV framework, with Susceptible, Exposed, Infectious, and Vaccinated classes (Figure 4.1). Dog demography governs the dynamics of the susceptible and vaccinated classes. The Susceptible population is replenished by births and depleted by mortality (both natural and disease-induced) and vaccination. The Vaccinated population is governed by the rate of vaccination, but depleted by natural mortality and waning of immunity generated by vaccines (most high quality vaccines are protective for at least 3 years, [10]. For canine rabies, evidence suggests that domestic dogs are the reservoir host even in areas with complex wild carnivore communities [11], [12]. While other wildlife hosts may contribute to transmission, single-host models of rabies in the dog population are likely sufficient to understanding and predicting dynamics in most endemic areas [13].
Rabies virus is directly transmitted, typically via bites, in the saliva of infectious animals. Transmission is on average low: most dogs do not transmit or only infect one or two other dogs. However, there is also substantial heterogeneity in transmission, and some dogs are capable of biting upwards of 20 other dogs during their short infectious period [14]. The incubation period is about 21 days but is highly variable. Most exposed dogs become infectious within one month, but some infections manifest months after initial exposure [14]-[16]. The infectious period, on the other hand, is predictably short, and infection results in death generally within 10 days of showing neurological signs of infection [14], [17]. There is little evidence that individuals can be infectious but sub-clinical (i.e. no carrier class), and there is no recovered class, as exposure does not confer immunity [18], and following onset of clinical signs, rabies is invariably fatal.
Although transmission is mostly local (< 1 km), rabies can cause erratic and unpredictable behavior, with infected dogs able to run more than 15 km, beyond the typical home range of most healthy dogs [14]. As a result, secondary cases often occur from disease-mediated incursions spread from neighboring populations (e.g., nearby populated settlements within the range of rabid dog movement). In addition, long-distance human-mediated incursions of incubating dogs can result in outbreaks being seeded from otherwise unconnected populations [19].
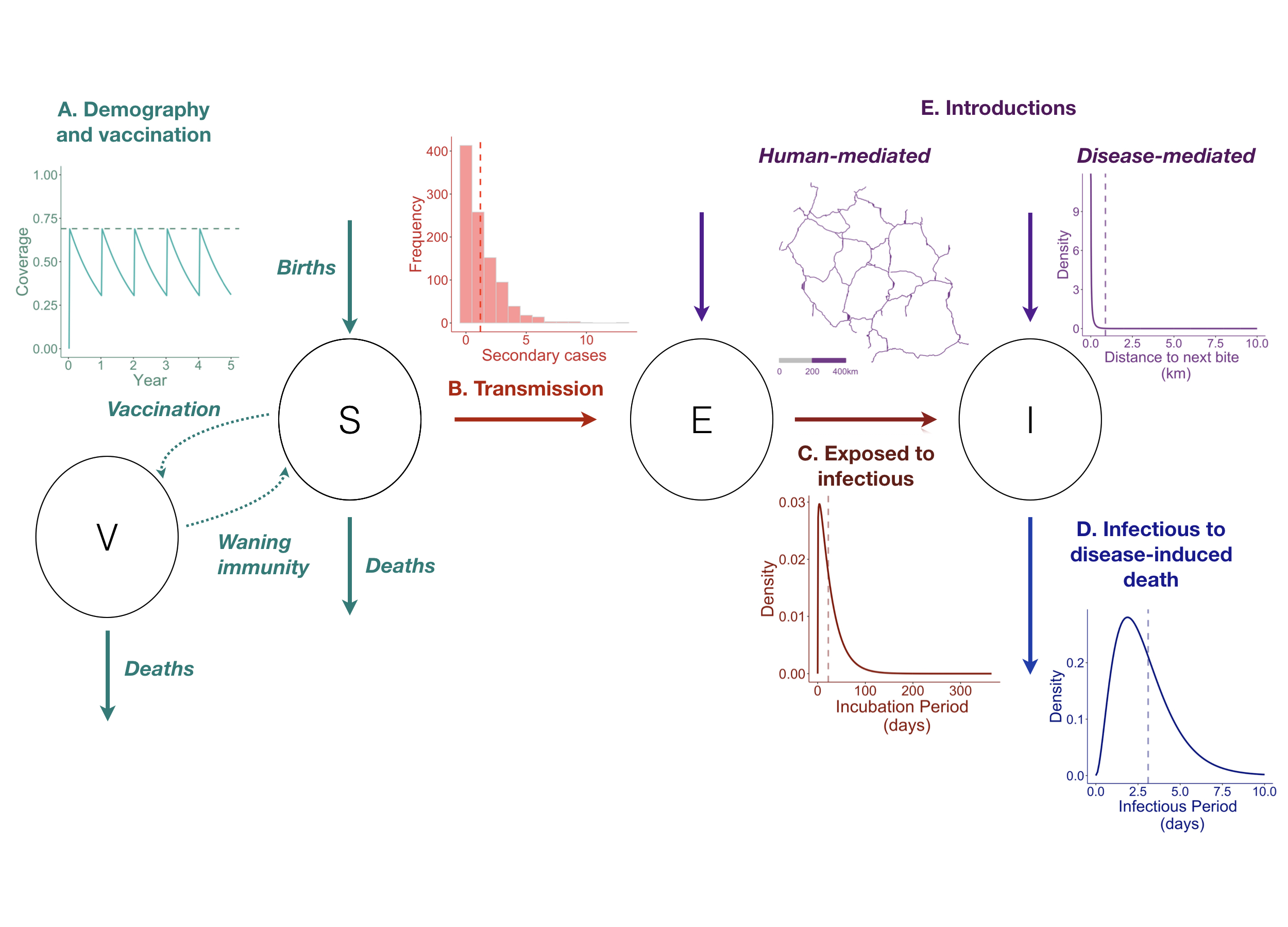
Figure 4.1: (ref:ch4-fig1-cap)
(ref:ch4-fig1-cap) The Susceptible-Exposed-Infectious-Vaccinated (SEIV) modeling framework for canine rabies: circles indicate epidemiological classes, arrows linking circles indicate how individuals can move between classes, insets describe underlying processes and influences. A) Host demography (i.e., the balance between births and deaths) and vaccination govern the susceptible and vaccinated population dynamics. Following vaccination campaigns, vaccination coverage (y axis, inset) first increases (vertical jumps) then wanes over time (x axis) as vaccinated individuals die, susceptible individuals are born, or as immunity conferred by vaccination wanes (in this example, campaigns reach 70% of the population annually, but coverage wanes to approximately 35% before the next annual campaign). B) Transmission is on average low, but highly heterogeneous. Inset shows number of secondary cases generated from a negative binomial distribution (n = 1000 draws, mean number of secondary cases = 1.2, red dashed line). C) Individuals move from exposed to infectious on average after 22.3 days (inset, dashed line) but this is also highly variable with some infections occurring months to years after exposure. D) Disease-induced mortality is complete, and the infectious period is short, on average 3.1 days (dashed line), with deaths due to infection occurring within 10 days. E) Introductions from outside the population modeled may seed cases within. Introductions may results from disease-mediated movement of infectious dogs (sometimes upwards of 10 km; inset shows dispersal kernel, gamma distribution) and human-mediated movements of incubating dogs (potentially on the scale of 100s of km through movement along roads; the inset shows an example of a major road network in Tanzania). All parameters used and associated references are listed in Table 4.1
| Process | Distribution | Parameters | Value | Source | Inset |
|---|---|---|---|---|---|
| Birth rate | – | Mean annual rate (dogs/yr) | 0.5 | [20] | A |
| Death rate | – | Mean annual rate (dogs/yr) | 0.42 | [20] | A |
| Vaccine waning | – | Mean annual rate (dogs/yr) | 0.33 | [10] | A |
| Secondary cases (R0) | Negative binomial, mean 1.2 secondary cases | Mean | 1.2 | Townsend et al., 2013 | B |
| Dispersion parameter (k) | 1.3 | ||||
| Incubation period | Gamma, mean 22.3 days | Shape | 1.15 | Hampson et al., 2009 | C |
| Rate | 0.04 | ||||
| Infectious period | Gamma, mean 3.1 days | Shape | 2.9 | Hampson et al., 2009 | D |
| Rate | 1.01 | ||||
| Dispersal kernel | Gamma, mean 0.88 km | Shape | 0.215 | Townsend et al., 2013 | E |
| Rate | 0.245 |
4.2 How to model rabies virus transmission?
There has been considerable debate about how to model rabies virus transmission, which echoes a larger debate within the disease ecology community [21]. Theory indicates that for diseases with density-dependent transmission, i.e. when transmission scales with host density, there exists a threshold density below which the disease cannot persist [22]. However, there is no such threshold when transmission is frequency-dependent, i.e. transmission rates are independent of host density [21].
For canine rabies, the basic reproductive number (Ro) or the average number of secondary cases resulting from a single infection in a completely susceptible population, is generally estimated as between 1-2 [14], [23]-[25]. Such consistently low estimates of R0 across a range of dog densities suggest that rabies virus transmission is largely frequency-dependent [14], [24], [26]-[28]. That is, rabid dogs have on average the same number of infectious contacts regardless of the density of dogs around them. As a result, reductions in population densities are not likely to be effective in eliminating rabies. In practice, although a common practice and one predicated on assumptions of density-dependent transmission, indeterminate culling of dogs does not curtail rabies transmission [29].
Despite evidence for frequency-dependent transmission, many modeling studies formulate rabies transmission as density-dependent (Fig 4.2D). For a given R0, this assumption of density-dependent transmission does not impact herd immunity thresholds; the critical proportion that needs to be vaccinated, pc, is equal to 1 - 1/R0 regardless of the form of transmission [22]. However density-dependent models predict reductions in transmission due to declining dog density (e.g., via culling or disease-induced mortality) that are unlikely to translate to the real world.
Models with frequency-dependent transmission are also not entirely consistent with empirical observations. Frequency-dependent models that assume homogeneous mixing (i.e. equal contact probabilities between all individuals in a population, also referred to as ‘mass action’) result in eventual population extinction for fatal pathogens like rabies [30]. Only under very low transmission (1.01-1.02) and high population growth can rabies persist in models with frequency-dependent transmission. For models with density-dependent transmission, even with R0 between 1.01 and 1.1, models of rabies show high annual incidence (Figure 4.4), which is at odds with empirical evidence. Where measured, rabies incidence is low (< 1-2% annually) and consequently has little demographic impact on dog populations [31]. Additional model structure is therefore necessary to explain how rabies can persist at such low incidence.
Transmission heterogeneity may be a potential mechanism to explain the relatively low incidence of rabies. A high proportion of dead-end or singleton transmissions result in negligible depletion of susceptibles, while occasional super-spreaders may seed and maintain transmission. In addition to unrealistic estimates of rabies incidence, if heterogeneity in transmission is not captured, there is a risk that models may generate biased estimates of control indicators, such as the time to elimination and the threshold level of vaccination that this requires.
Accounting for the spatial scale of transmission could also explain how rabies persists at low incidence. As most transmission occurs within a 1 km radius of infected animals, susceptible depletion at such fine scales may limit transmission in a way that is not captured in mass action models [32]. Phenomenological approximations may offer a solution to this challenge [33], [34], but have yet to be thoroughly explored for rabies. Spatially-explicit individual-based models implemented at the scale at which most mixing occurs generate more realistic dynamics [24], [35], but are computationally intensive and not analytically tractable. Nonetheless, such models provide insights into underlying mechanisms that could be simplified for more expedient models. Finally, human behavior has also been implicated in curtailing epidemics, with responses such as tying and killing infectious dogs and reactive vaccination thought to scale with incidence [36].
There is limited data to disentangle these potential mechanisms, which could reconcile empirical observations with modeling results. Further work is necessary to ensure sufficient model realism to inform policy, but balancing realism and complexity is a key challenge for any modeling study [37]. Building in realism requires additional parameterization and, often, additional assumptions. Robust epidemiological and biological data are therefore key to improving our understanding of how to model rabies transmission.
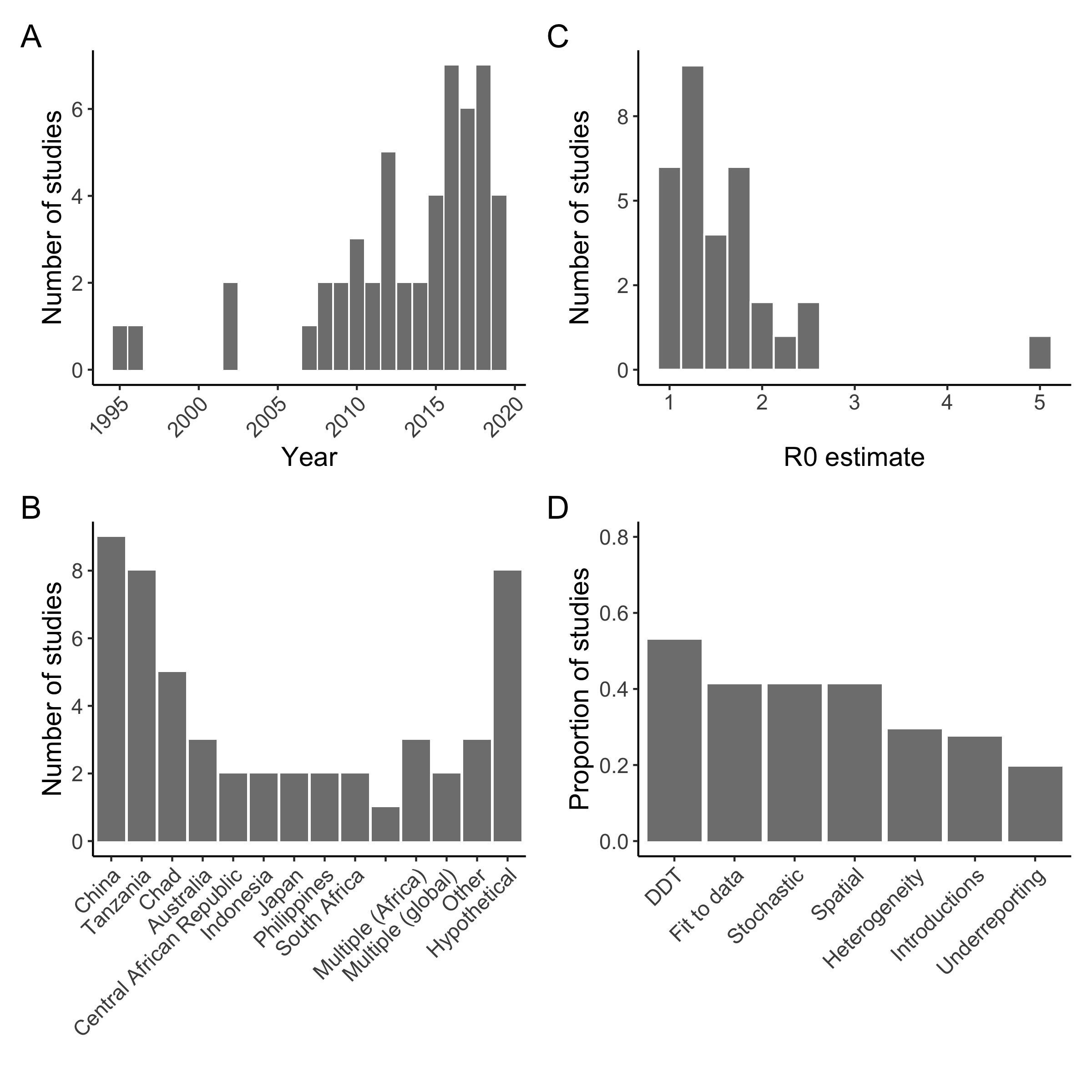
Figure 4.2: (ref:ch4-fig2-cap)
(ref:ch4-fig2-cap) Summary of studies with a dynamic model of canine rabies. A total of 51 studies were included. A) Year of publication, with most studies published after 2006; B) Countries where rabies dynamics were modeled: studies were concentrated in China, Tanzania, and Chad, but many also examined dynamics in hypothetical contexts, not specific to any geographic situation. C) Estimates of R0: most studies estimated R0 below 2 (10 studies, with 31 estimates; estimates of Re (the effective reproduction number which accounts for ongoing vaccination) and Rt (time-varying reproductive number) were excluded (N = 3). D) Key features of models (N = 51): most assumed density-dependent transmission (N = 27). Less than half were fit to data (N = 20), stochastic (N = 20), or spatially-explicit (N = 19). 15/51 studies incorporated individual heterogeneity in transmission and 14/51 introductions from outside the population modeled. Only 10 included an observation model in their analysis or accounted for under-reporting in their inference. Full bibliography and metadata included in Supplementary Table 1.
4.3 Existing Modeling Studies
Two systematic reviews of rabies models recently examined the effectiveness and cost-effectiveness of control and prevention strategies. They concluded that estimates of R0 are consistently below 2 and dog vaccination is an effective strategy, but vaccination coverage is critically influenced by dog demography [38]. Both mass dog vaccination and provisioning of PEP to bite patients are cost-effective, in contrast to dog culling which has rarely been identified as either economically feasible or effective [39]. Building off these reviews, we examined studies with a dynamic modeling component and synthesized insights generated and data used to inform them. We searched for papers that had the terms “rabies” AND (“domestic dog*” OR “canine”) AND “model*” on PubMed and Scopus, including all English language papers published between January 1995 and July 2019 that incorporated a transmission model of rabies virus in domestic dogs. Of the 547 unique records retrieved, 51 papers fitted these inclusion criteria (Fig 4.3, Online Supplementary Table S1).
4.3.1 Insights and limitations
Of studies that compared intervention strategies (generally: mass dog vaccination, human PEP provisioning, and dog population control including culling), the majority show that dog vaccination is most effective, and essential to achieve elimination. Despite the potential to maximize population-level immunity, synchronizing vaccination campaigns geographically had little impact on probability of elimination, at least for annual vaccination campaigns. In contrast, spatial heterogeneity in vaccination coverage had a greater impact, with even small contiguous coverage gaps reducing the probability of rabies being eliminated [24], [35].
While the critical vaccination threshold (pc or 1 - 1/Ro) should theoretically be much lower than 70% for a disease with the low range of R0 estimated for rabies (Figure 4.2C), the coverage level recommended by WHO reflects an empirical consensus [23], [40]. Models show that due to high turnover in domestic dog populations, annual campaigns that reach at least 70% of the population are necessary to maintain coverage > 20% throughout the year. Furthermore, heterogeneity in transmission and frequent introductions of rabies cases increase both the vaccination threshold necessary to interrupt transmission, and the probability of observing small outbreaks even when vaccination coverage is high [14], [41].
Most published models were deterministic (33/51) and did not incorporate heterogeneities in transmission (36/51, Figure 4.2D). However, as R0 for rabies appears to be low, the interaction between stochasticity and heterogeneity in transmission may be influential. In general, for diseases with high transmissibility (i.e. measles), heterogeneities in transmission can often be ignored as these complexities have little impact on the emergent dynamics of infection [30]. However, for a disease with lower transmission, heterogeneities may result in unpredictable outbreaks [37]. Stochasticity is especially crucial in the endgame, when elimination probabilities and incursion dynamics depend on rare events.
Most studies model rabies virus transmission in a closed population, that is without introductions from neighboring areas (Figure 4.2D). While this is a reasonable approach in island settings such as in Bali, Indonesia [24], recent modeling and phylogenetic work shows the importance of incursions in less isolated populations in sustaining rabies virus transmission (Bourhy et al., 2016; Zinsstag et al., 2017) and that multiple strains co-circulate within a population [42], [43]. Human behavior is also a key driver of transmission patterns, facilitating as well as dampening transmission [44]. Multiple studies have found signals of long distance transmission beyond the range of disease-mediated dispersal, showing the role of human-mediated movement of incubating dogs [44]-[46]. Road networks have been identified as correlates of phylogenetic distance, indicating that human movement could shape the spatial structure of canine rabies virus [44]-[46]. There is also strong pyhlogenetic evidence that historical human-mediated long-distance movements underlie much of the contemporary global distribution of canine rabies [47]. This work emphasizes the need to understand how the size and connectivity of populations affects the persistence of disease. Models have productively explored this historically important question for childhood infections such as measles [48], but for canine rabies, this remains an important challenge, which may well define progress towards elimination.
A few studies look at how contact networks and movement behaviors could drive transmission [49]-[51]. These studies simulated outbreaks on contacts networks constructed using data from healthy domestic dogs. They found that in general, targeting highly connected dogs or dogs with larger home ranges for vaccination results in a higher probability of disease elimination, but few predictors of connectivity of individuals emerged. Broadly, these results are consistent with previous work on transmission heterogeneity and could bring valuable benefits if it were possible to a priori identify and target high-risk animals. However, these traits are difficult to estimate in most endemic settings, where there is limited data on dog populations, let alone individual dog traits. Moreover, as rabies causes severe neurological symptoms, the validity of these findings depends on how representative data from healthy dogs are of movement and contact patterns of rabid dogs.
Dynamic models have been integrated with economic models to estimate cost-effectiveness of interventions, demand for rabies PEP, and disease burden. Early cost-effectiveness models critically lacked data on the costs of PEP for those seeking care for non-rabid dog bites [27], [52], [53]. Decision tree models have addressed these issues and provide a framework to integrate field data on rabies exposures, health-seeking, and access and adherence to PEP into estimates of burden [54]-[56]. These more recent studies demonstrate that PEP is still a very cost-effective intervention even when accounting for management of patients bitten by non-rabid animals and emphasize the potential value of administering rabies vaccine intradermally using the latest WHO recommended abridged regimens [57]. However, they also highlight two other critical points for policy. First, without strategies for more judicious use, costs of PEP will remain high and continue to rise even when dog rabies is controlled. Moreover, human rabies deaths will continue to occur and the target of zero deaths by 2030 cannot be achieved through PEP alone. A massive scaling up of dog vaccination is required in most endemic countries. Support for human rabies vaccines through Gavi, the Vaccine Alliance, is therefore a promising step towards the 2030 goal [56], but more investment and commitment is still needed.
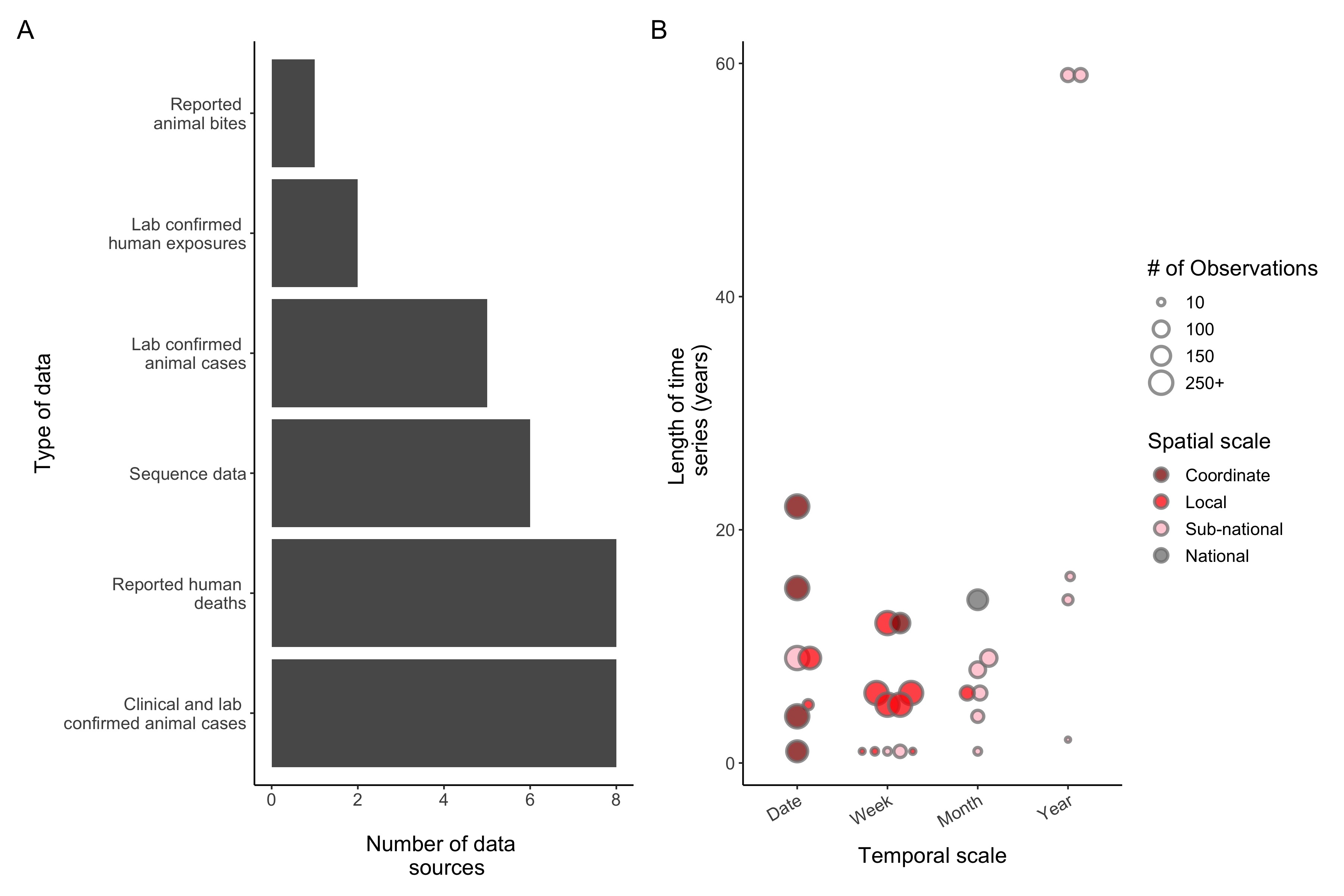
Figure 4.3: (ref:ch4-fig3-cap)
(ref:ch4-fig3-cap) Rabies data reported in modeling studies (N = 25 studies reporting 30 unique data sources). A) Type of data used. B) The scales of temporal (x-axis) and spatial (colors) information available and the duration (y axis). The size of the points is proportional to the number of observations in each data set. Any rabies data that was reported in studies were included (even if not used for fitting purposes, only for qualitative comparison). If multiple data sets were used, they were included as separate data sources, and if the same data set was used in multiple studies it was only included once.
4.4 The gap between models and data
Despite limited surveillance, few studies incorporated observation models into their analyses or conducted sensitivity analyses on how under-reporting might bias their inferences (Figure 4.2D). Developing models of the observation process and integrating them into dynamic models (often termed state-space modeling, [58]-[60] is essential when fitting to incomplete data. But, these modeling frameworks can also guide surveillance strategies across the elimination timeline by estimating the minimum detection levels and time necessary to verify elimination [61].
A major limitation of many existing modeling studies is a lack of data to inform conclusions, with less than 40% of models fit to data (Fig 4.2D). For studies which did report incidence data, the scale and quality of the data also varied greatly. Human deaths reported at the national or regional level and numbers of clinical and laboratory confirmed animal cases were the most commonly used data (Figure 4.3A). The number of observations and length of the time series varied greatly, from over 1000+ observations at a fine spatiotemporal scale over a 15-year period to annual cases reported for only 2 years (Figure 4.3B). Ultimately, integrating data on rabies incidence and dog populations into models of transmission is a critical step to moving modeling efforts forward. Below we describe the various data sources that can be used to fit and inform models and associated challenges and solutions to collecting this data.
4.4.1 Bite data
Bite data, (i.e. data on patients seeking care for animal bites) are often used as a proxy for rabies exposure incidence. However, these data often lack details on the status of the biting animal and are heavily skewed by who has access to care, both geographically and socioeconomically. Paradoxically, in settings where the direct cost of PEP is charged to patients, bite records may be more reflective of rabies exposures: people may be less likely to seek care when the perceived risk is low (i.e. fewer people seek care for provoked bites by known healthy and/or vaccinated animals) due to the associated costs [62], [63]. In settings where PEP is provided for free and indiscriminately, a higher proportion of reported bites may be due to non-rabid animals [64]-[66], and many Category 1 exposures, i.e. those for which PEP is not indicated [67], receive unnecessary PEP [66], [68], [69].
For data on bite patients to be more useful for modeling and surveillance purposes, supplementary information for each bite beyond the date reported and number of doses received is needed. Categorizing the type of exposure per the WHO categories can help to exclude Category 1 exposures. Reporting clinical signs and the outcome of the biting animal at each patient visit can identify probable rabies exposures and trigger field investigations and sample collection to improve surveillance. Finally, information on the geographical location where the patient was bitten, for example to the finest scale administrative unit identifiable, could be used to understand spatial patterns of transmission, estimate demand for PEP, and identify determinants of health seeking behavior.
4.4.2 Laboratory confirmed case data
Laboratory confirmed case data are considered a gold standard due to the high sensitivity and specificity of diagnostic tests for rabies, but represent the tip of the iceberg in terms of true incidence [9], [61]. Diagnostic confirmation of rabies cases is often lacking in many endemic settings due to limited laboratory and field capacity. Even with strong laboratory resources in country, collecting a brain sample from a suspected rabid animal or human case can be challenging. Lack of cold chain and accessibility to communities, limited veterinary capacity and training in euthanasia and sampling methods, and low reporting of suspected cases are all significant barriers to case confirmation. For humans, nuchal samples can be collected non-invasively (from nape of the neck) to confirm a rabies case ante-mortem [70]. However, confirmation of a human case first requires a person to seek care, and rabies deaths are most common in populations with the least access to health care [71]. For animal cases, field sample collection methods, like the straw method of sampling brain tissue that does not require the submission of the whole head, and alternative forms of sample storage and testing, such as rapid diagnostic tests and filter papers, have potential to address some of these challenges [72]. While these alternative tests may not be appropriate for guiding patient treatment, they could greatly improve surveillance and understanding of rabies virus transmission if implemented more routinely.
Even with the gold-standard diagnostic test, using laboratory confirmation to guide administration of PEP in endemic settings may be impractical, due to delays in sampling and testing. Integrated bite case management (IBCM, see Chapter 18) programs, which combine risk assessments, field investigations, animal observation/quarantine, and sampling of suspected cases, are a promising method of improving rabies surveillance and PEP provisioning. IBCM can increase both detection of and confirmation of clinically suspect animal cases and guide referrals for PEP , as well as limit further exposures by euthanizing rabid animals once detected [73]. However, IBCM relies on coordination between human and animal health practitioners and resources to support clinical rabies diagnosis and field sample collection, which is still lacking in most low-income countries.
4.4.3 Sequence data
Sequence data can be used to make inferences about transmission processes, particularly when linked with epidemiological data [43]-[45], [60], [74], [75]. Recent studies have demonstrated the added value of whole-genome sequencing (WGS) for understanding finer scale transmission dynamics of canine rabies [44], [74], but WGS has yet to be routinely generated for canine rabies. Sequencing capacity is even more limited than general laboratory capacity in rabies-endemic countries and exporting samples for sequencing is costly. Advances in portable, real-time sequencing could help to tackle these limitations in the field (ARTICnetwork, http://artic.network/index.html). Portable sequencers such as the MinION could support rapid generation and dissemination of sequence data. Methods to sequence from alternative sample types, such as rapid diagnostic tests and filter papers, could also help to overcome obstacles in field sample collection and transport [72]. Bioinformatic pipelines and open sharing of sequences, such as those developed for other viral pathogens [76], could greatly facilitate our understanding of rabies dynamics at a regional and global scale. In general, low-cost, high-throughput sequencing methods should be developed to increase the timely availability of representative sequence data from endemic settings.
4.4.4 Dog population and vaccination data
Data on the dog population is necessary to further understand how the distribution, density, and connectivity of the host population drives transmission [74]. Estimates of vaccination coverage and other intervention efforts facilitate inference of the mechanisms driving transmission and the impact of interventions, helping to predict future outcomes given different control strategies [75]. In most endemic countries, limited systematic data is collected on dog populations. If integrated into more routine census or demographic surveys (i.e. the Demographic and Health Surveys, https://dhsprogram.com), questions on dog ownership and vaccination status at the household level could be a potential way to get this data where the majority of the dog population is owned. However, if conducted as standalone surveys, these can be resource intensive and difficult to implement in a representative way, particularly in more rural/remote areas. Alternatively, integrating post-vaccination coverage surveys into campaigns has been shown to be a cost-effective way to generate coverage and population estimates, and only requires temporary marking of vaccinated dogs [77]-[79]. As spatial heterogeneity in coverage is likely a key factor driving the success of vaccination campaigns, such coverage estimates at the scale at which campaigns are implemented could be critical to understanding rabies persistence and elimination probabilities.
4.5 Conclusions
Modeling studies, in combination with decades of empirical evidence, have demonstrated that dog vaccination is the optimal intervention strategy for controlling canine rabies. As global momentum for implementing national rabies control programs grows, models should move beyond comparing vaccination and other strategies in idealized populations towards linking models with field data to identify refinements to intervention strategies. To date, most work has focused on studying control efforts and identifying drivers of dynamics (often without using data), and studies of the impact of control have rarely been linked to analyses grounded in empirical data (i.e. studies that explained observed patterns or estimated key parameters, see Figure 4.5 for an overview of existing studies). Models should aim to integrate these questions and test specific vaccination strategies, such as ring vaccination or establishment of control corridors based on geographic barriers as implemented for wildlife rabies in Europe.
Key parameters to estimate from models and data include transmission heterogeneity (captured in the distribution of secondary cases), the dispersal kernel, and introduction rates (including how to differentiate ongoing local transmission from imported cases). Integrating models of surveillance into dynamic models can further establish surveillance requirements necessary to verify freedom from disease and inform policy decisions regarding the cessation and scaling back of control efforts. Importantly, models can predict how these requirements might change over the elimination timeline. Given the challenges in generating high-quality surveillance data for canine rabies, these models can also be used to account for under-reporting and determine the minimum level of detection necessary for robust inference. Phylodynamic approaches, which combine both epidemiological and genetic data, are a promising avenue to tackle many of these questions. Critically, progress in this area will require strong surveillance systems and representative data from a range of populations.
Countries have made varying progress towards elimination, ranging from some that lack a realized national control policy and others in the end-game stages of elimination. Now, we are tasked with building flexible models that can capture rabies dynamics and the impacts of control across the elimination timeline. Identifying where and how implementation of control efforts needs improving and delivering such improvements will require a much closer collaboration between scientists, practitioners and policymakers.
4.6 Data and code availability
All data and code used to generate figures and supplemental files, as well as the bibliography for the literature review are available online at https://github.com/mrajeev08/ModelingChapter.
4.7 References
[1] H. Heesterbeek, R. M. Anderson, V. Andreasen, S. Bansal, D. De Angelis, C. Dye, K. T. D. Eames, W. J. Edmunds, S. D. W. Frost, S. Funk, T. D. Hollingsworth, T. House, V. Isham, P. Klepac, J. Lessler, J. O. Lloyd-Smith, C. J. E. Metcalf, D. Mollison, L. Pellis, J. R. C. Pulliam, M. G. Roberts, C. Viboud, Isaac Newton Institute IDD Collaboration, “Modeling infectious disease dynamics in the complex landscape of global health,” Science, vol. 347, no. 6227, pp. aaa4339–aaa4339, Mar. 2015.
[2] P. Klepac, C. J. E. Metcalf, A. R. McLean, and K. Hampson, “Towards the endgame and beyond: complexities and challenges for the elimination of infectious diseases,” Philosophical Transactions of the Royal Society B: Biological Sciences, vol. 368, no. 1623, pp. 20120137–20120137, Jun. 2013.
[3] V. G. Panjeti and L. A. Real, “Mathematical models for rabies.,” Adv. Virus Res., vol. 79, pp. 377–395, 2011.
[4] R. M. Anderson, H. C. Jackson, R. M. May, and A. M. Smith, “Population dynamics of fox rabies in Europe,” Nature, vol. 289, no. 5800, pp. 765–771, Feb. 1981.
[5] J. D. Murray, E. A. Stanley, and D. L. Brown, “On the spatial spread of rabies among foxes,” Proceedings of the Royal Society of London. Series B. Biological Sciences, vol. 229, no. 1255, pp. 111–150, Nov. 1986.
[6] D. L. Smith, B. Lucey, L. A. Waller, J. E. Childs, and L. A. Real, “Predicting the spatial dynamics of rabies epidemics on heterogeneous landscapes.,” Proc Natl Acad Sci USA, vol. 99, no. 6, pp. 3668–3672, Mar. 2002.
[7] S. M. Duke-Sylvester, L. Bolzoni, and L. A. Real, “Strong seasonality produces spatial asynchrony in the outbreak of infectious diseases,” Journal of The Royal Society Interface, vol. 8, no. 59, pp. 817–825, Jan. 2011.
[8] S. Cleaveland, H. Beyer, K. Hampson, D. Haydon, F. Lankester, T. Lembo, F.-X. Meslin, M. Morters, Z. Mtema, M. Sambo, and S. Townsend, “The changing landscape of rabies epidemiology and control.,” Onderstepoort J. Vet. Res., vol. 81, no. 2, pp. E1–8, Apr. 2014.
[9] T. P. Scott, A. Coetzer, A. S. Fahrion, and L. H. Nel, “Addressing the Disconnect between the Estimated, Reported, and True Rabies Data: The Development of a Regional African Rabies Bulletin,” Front Vet Sci, vol. 4, no. 4, pp. 1–6, Feb. 2017.
[10] N. Lakshmanan, T. C. Gore, K. L. Duncan, M. J. Coyne, M. A. Lum, and F. J. Sterner, “Three-year rabies duration of immunity in dogs following vaccination with a core combination vaccine against canine distemper virus, canine adenovirus type-1, canine parvovirus, and rabies virus.,” Vet. Ther., vol. 7, no. 3, pp. 223–231, 2006.
[11] T. Lembo, D. T. Haydon, A. Velasco-Villa, C. E. Rupprecht, C. Packer, P. E. Brandão, I. V. Kuzmin, A. R. Fooks, J. Barrat, and S. Cleaveland, “Molecular epidemiology identifies only a single rabies virus variant circulating in complex carnivore communities of the Serengeti.,” Proceedings of the Royal Society B: Biological Sciences, vol. 274, no. 1622, pp. 2123–2130, Sep. 2007.
[12] T. Lembo, K. Hampson, D. T. Haydon, M. Craft, A. Dobson, J. Dushoff, E. Ernest, R. Hoare, M. Kaare, T. Mlengeya, C. Mentzel, and S. Cleaveland, “Exploring reservoir dynamics: a case study of rabies in the Serengeti ecosystem.,” J Appl Ecol, vol. 45, no. 4, pp. 1246–1257, Aug. 2008.
[13] S. Cleaveland, F. Lankester, S. Townsend, T. Lembo, and K. Hampson, “Rabies control and elimination: a test case for One Health.,” Vet. Rec., vol. 175, no. 8, pp. 188–193, Aug. 2014.
[14] K. Hampson, J. Dushoff, S. Cleaveland, D. T. Haydon, M. Kaare, C. Packer, and A. Dobson, “Transmission dynamics and prospects for the elimination of canine rabies.,” PLOS Biol, vol. 7, no. 3, p. e53, Mar. 2009.
[15] C. M. Foggin, “Rabies and rabies-related viruses in Zimbabwe: Historical, virological and ecological aspects,” Jan. 1988.
[16] T. Hemachudha, J. Laothamatas, and C. E. Rupprecht, “Human rabies: a disease of complex neuropathogenetic mechanisms and diagnostic challenges,” Lancet Neur, vol. 1, no. 2, pp. 101–109, Jun. 2002.
[17] V. Tepsumethanon, H. Wilde, and F. X. Meslin, “Six criteria for rabies diagnosis in living dogs.,” J Med Assoc Thai, vol. 88, no. 3, pp. 419–422, Mar. 2005.
[18] Y.-Z. Zhang, Z. F. Fu, D.-M. Wang, J.-Z. Zhou, Z.-X. Wang, T.-F. Lv, C.-L. Xiong, Y. Zou, W.-R. Yao, M.-H. Li, G.-M. Dong, G.-L. Xu, M. Niezgoda, I. V. Kuzmin, and C. E. Rupprecht, “Investigation of the Role of Healthy Dogs as Potential Carriers of Rabies Virus,” Vector-Borne and Zoonotic Diseases, vol. 8, no. 3, pp. 313–320, Jun. 2008.
[19] K. Brunker, K. Hampson, D. L. Horton, and R. Biek, “Integrating the landscape epidemiology and genetics of RNA viruses: rabies in domestic dogs as a model.,” Parasitology, vol. 139, no. 14, pp. 1899–1913, Dec. 2012.
[20] A. M. Czupryna, J. S. Brown, M. A. Bigambo, C. J. Whelan, S. D. Mehta, R. M. Santymire, F. J. Lankester, and L. J. Faust, “Ecology and Demography of Free-Roaming Domestic Dogs in Rural Villages near Serengeti National Park in Tanzania,” PLoS ONE, vol. 11, no. 11, p. e0167092, Nov. 2016.
[21] J. O. Lloyd-Smith, P. C. Cross, C. J. Briggs, M. Daugherty, W. M. Getz, J. Latto, M. S. Sánchez, A. B. Smith, and A. Swei, “Should we expect population thresholds for wildlife disease?,” Trends in Ecology & Evolution, vol. 20, no. 9, pp. 511–519, Sep. 2005.
[22] H. McCallum, N. Barlow, and J. Hone, “How should pathogen transmission be modelled?,” Trends in Ecology & Evolution, vol. 16, no. 6, pp. 295–300, Jun. 2001.
[23] P. G. Coleman and C. Dye, “Immunization coverage required to prevent outbreaks of dog rabies,” Vaccine, 1996.
[24] S. E. Townsend, I. P. Sumantra, Pudjiatmoko, G. N. Bagus, E. Brum, S. Cleaveland, S. Crafter, A. P. M. Dewi, D. M. N. Dharma, J. Dushoff, J. Girardi, I. K. Gunata, E. F. Hiby, C. Kalalo, D. L. Knobel, I. W. Mardiana, A. A. G. Putra, L. Schoonman, H. Scott-Orr, M. Shand, I. W. Sukanadi, P. P. Suseno, D. T. Haydon, and K. Hampson, “Designing programs for eliminating canine rabies from islands: Bali, Indonesia as a case study.,” PLoS Negl Trop Dis, vol. 7, no. 8, p. e2372, 2013.
[25] A. Kurosawa, K. Tojinbara, H. Kadowaki, K. Hampson, A. Yamada, and K. Makita, “The rise and fall of rabies in Japan: A quantitative history of rabies epidemics in Osaka Prefecture, 1914–1933,” PLoS Negl Trop Dis, vol. 11, no. 3, pp. e0005435–19, Mar. 2017.
[26] M. C. Fitzpatrick, K. Hampson, S. Cleaveland, L. A. Meyers, J. P. Townsend, and A. P. Galvani, “Potential for Rabies Control through Dog Vaccination in Wildlife-Abundant Communities of Tanzania,” PLoS Negl Trop Dis, vol. 6, no. 8, pp. e1796–6, Aug. 2012.
[27] J. Zinsstag, S. Durr, M. A. Penny, R. Mindekem, F. Roth, S. M. Gonzalez, S. Naissengar, and J. Hattendorf, “Transmission dynamics and economics of rabies control in dogs and humans in an African city,” Proc Natl Acad Sci USA, vol. 106, no. 35, pp. 1–22, Aug. 2009.
[28] H. Tian, Y. Feng, B. Vrancken, B. Cazelles, H. Tan, M. S. Gill, Q. Yang, Y. Li, W. Yang, Y. Zhang, Y. Zhang, P. Lemey, O. G. Pybus, N. C. Stenseth, H. Zhang, and S. Dellicour, “Transmission dynamics of re-emerging rabies in domestic dogs of rural China,” PLoS Pathog, vol. 14, no. 12, pp. e1007392–18, Dec. 2018.
[29] M. K. Morters, O. Restif, K. Hampson, S. Cleaveland, J. L. N. Wood, and A. J. K. Conlan, “Evidence-based control of canine rabies: a critical review of population density reduction,” J Anim Ecol, vol. 82, no. 1, pp. 6–14, Sep. 2012.
[30] M. J. Keeling and P. Rohani, Modeling infectious diseases in humans and animals. 2008.
[31] K. Hampson, B. Abela-Ridder, K. Brunker, S. T. M. Bucheli, M. Carvalho, E. Caldas, J. Changalucha, S. Cleaveland, J. Dushoff, V. Gutierrez, A. R. Fooks, K. Hotopp, D. T. Haydon, A. Lugelo, K. Lushasi, R. Mancy, D. Marston, Z. Mtema, M. Rajeev, L. R. M. P. Dourado, J. F. G. Roldan, K. Rysava, S. M. Rocha, M. Sambo, L. Sikana, M. Vigilato, and V. Del Rio Vilas, “Surveillance to Establish Elimination of Transmission and Freedom from Dog-mediated Rabies,” bioRxiv, p. 096883, Dec. 2016.
[32] M. J. Ferrari, S. E. Perkins, L. W. Pomeroy, and O. N. Bjørnstad, “Pathogens, Social Networks, and the Paradox of Transmission Scaling,” Interdisciplinary Perspectives on Infectious Diseases, vol. 2011, no. 2, pp. 1–10, 2011.
[33] J. P. Aparicio and M. Pascual, “Building epidemiological models from R0: an implicit treatment of transmission in networks,” Proceedings of the Royal Society B: Biological Sciences, vol. 274, no. 1609, pp. 505–512, Feb. 2007.
[34] M. Pascual, M. Roy, and K. Laneri, “Simple models for complex systems: exploiting the relationship between local and global densities,” Theor Ecol, vol. 4, no. 2, pp. 211–222, Mar. 2011.
[35] E. A. Ferguson, K. Hampson, S. Cleaveland, R. Consunji, R. Deray, J. Friar, D. T. Haydon, J. Jimenez, M. Pancipane, and S. E. Townsend, “Heterogeneity in the spread and control of infectious disease: consequences for the elimination of canine rabies,” Nature Publishing Group, vol. 5, no. 1, pp. 1–13, Dec. 2015.
[36] K. Hampson, J. Dushoff, J. Bingham, G. Brückner, Y. H. Ali, and A. Dobson, “Synchronous cycles of domestic dog rabies in sub-Saharan Africa and the impact of control efforts.,” Proc Natl Acad Sci USA, vol. 104, no. 18, pp. 7717–7722, May 2007.
[37] N. C. Grassly and C. Fraser, “Mathematical models of infectious disease transmission,” Nat Rev Micro, vol. 180, pp. 1–12, May 2008.
[38] W. Rattanavipapong, M. Thavorncharoensap, S. Youngkong, A. J. Genuino, T. Anothaisintawee, U. Chaikledkaew, and A. Meeyai, “The impact of transmission dynamics of rabies control: Systematic review.,” Vaccine, Dec. 2018.
[39] T. Anothaisintawee, A. Julienne Genuino, M. Thavorncharoensap, S. Youngkong, W. Rattanavipapong, A. Meeyai, and U. Chaikledkaew, “Cost-effectiveness modelling studies of all preventive measures against rabies: A systematic review.,” Vaccine, Dec. 2018.
[40] World Health Organization, “WHO Expert Consultation on Rabies. Second report.,” World Health Organ Tech Rep Ser, no. 982, pp. 1–139– back cover, 2013.
[41] J. O. Lloyd-Smith, S. J. Schreiber, P. E. Kopp, and W. M. Getz, “Superspreading and the effect of individual variation on disease emergence,” Nature, vol. 438, no. 7066, pp. 355–359, Nov. 2005.
[42] M. Laager, M. Léchenne, K. Naissengar, R. Mindekem, A. Oussiguere, J. Zinsstag, and N. Chitnis, “A metapopulation model of dog rabies transmission in N’Djamena, Chad,” Journal of Theoretical Biology, vol. 462, pp. 408–417, Feb. 2019.
[43] H. Bourhy, E. Nakouné, M. Hall, P. Nouvellet, A. Lepelletier, C. Talbi, L. Watier, E. C. Holmes, S. Cauchemez, P. Lemey, C. A. Donnelly, and A. Rambaut, “Revealing the Micro-scale Signature of Endemic Zoonotic Disease Transmission in an African Urban Setting,” PLoS Pathog, vol. 12, no. 4, pp. e1005525–15, Apr. 2016.
[44] K. Brunker, D. A. Marston, D. L. Horton, S. Cleaveland, A. R. Fooks, R. Kazwala, C. Ngeleja, T. Lembo, M. Sambo, Z. J. Mtema, L. Sikana, G. Wilkie, R. Biek, and K. Hampson, “Elucidating the phylodynamics of endemic rabies virus in eastern Africa using whole-genome sequencing.,” Virus Evol, vol. 1, no. 1, pp. vev011–11, 2015.
[45] C. Talbi, P. Lemey, M. A. Suchard, E. Abdelatif, M. Elharrak, N. Jalal, A. Faouzi, J. E. Echevarría, S. Vazquez Morón, A. Rambaut, N. Campiz, A. J. Tatem, E. C. Holmes, and H. Bourhy, “Phylodynamics and Human-Mediated Dispersal of a Zoonotic Virus,” PLoS Pathog, vol. 6, no. 10, pp. e1001166–10, Oct. 2010.
[46] K. Tohma, M. Saito, C. S. Demetria, D. L. Manalo, B. P. Quiambao, T. Kamigaki, and H. Oshitani, “Molecular and mathematical modeling analyses of inter-island transmission of rabies into a previously rabies-free island in the Philippines,” INFECTION, GENETICS AND EVOLUTION, vol. 38, no. C, pp. 22–28, Mar. 2016.
[47] A. A. King, A. R. Fooks, M. Aubert, and A. I. Wandeler, Historical perspective of rabies in Europe and the Mediterranean Basin. 2004.
[48] O. N. Bjørnstad and B. T. Grenfell, “Hazards, spatial transmission and timing of outbreaks in epidemic metapopulations,” Environ Ecol Stat, vol. 15, no. 3, pp. 265–277, Dec. 2008.
[49] M. Laager, C. Mbilo, E. A. Madaye, A. Naminou, M. Léchenne, A. Tschopp, S. K. Naïssengar, T. Smieszek, J. Zinsstag, and N. Chitnis, “The importance of dog population contact network structures in rabies transmission,” PLoS Negl Trop Dis, vol. 12, no. 8, p. e0006680, Aug. 2018.
[50] E. G. Hudson, V. J. Brookes, M. P. Ward, and S. Dürr, “Using roaming behaviours of dogs to estimate contact rates: the predicted effect on rabies spread,” Epidemiol. Infect., vol. 147, p. e135, Jan. 2019.
[51] J. K. Wilson-Aggarwal, L. Ozella, M. Tizzoni, C. Cattuto, G. J. F. Swan, T. Moundai, M. J. Silk, J. A. Zingeser, and R. A. McDonald, “High-resolution contact networks of free-ranging domestic dogs Canis familiaris and implications for transmission of infection.,” PLoS Negl Trop Dis, vol. 13, no. 7, p. e0007565, Jul. 2019.
[52] K. Hampson, S. Cleaveland, and D. Briggs, “Evaluation of Cost-Effective Strategies for Rabies Post-Exposure Vaccination in Low-Income Countries,” PLoS Negl Trop Dis, vol. 5, no. 3, p. e982, Mar. 2011.
[53] M. C. Fitzpatrick, K. Hampson, S. Cleaveland, I. Mzimbiri, F. Lankester, T. Lembo, L. A. Meyers, A. D. Paltiel, and A. P. Galvani, “Cost-effectiveness of canine vaccination to prevent human rabies in rural Tanzania.,” Ann. Intern. Med., vol. 160, no. 2, pp. 91–100, Jan. 2014.
[54] D. L. Knobel, S. Cleaveland, P. G. Coleman, E. M. Fèvre, M. I. Meltzer, M. E. G. Miranda, A. Shaw, J. Zinsstag, and F.-X. Meslin, “Re-evaluating the burden of rabies in Africa and Asia.,” Bull. World Health Organ., vol. 83, no. 5, pp. 360–368, May 2005.
[55] K. Hampson, L. Coudeville, T. Lembo, M. Sambo, A. Kieffer, M. Attlan, J. Barrat, J. D. Blanton, D. J. Briggs, S. Cleaveland, P. Costa, C. M. Freuling, E. Hiby, L. Knopf, F. Leanes, F.-X. Meslin, A. Metlin, M. E. Miranda, T. Müller, L. H. Nel, S. Recuenco, C. E. Rupprecht, C. Schumacher, L. Taylor, M. A. N. Vigilato, J. Zinsstag, J. Dushoff, Global Alliance for Rabies Control Partners for Rabies Prevention, “Estimating the global burden of endemic canine rabies.,” PLoS Negl Trop Dis, vol. 9, no. 4, p. e0003709, Apr. 2015.
[56] WHO Rabies Modelling Consortium, “The potential impact of improved provision of rabies post-exposure prophylaxis in Gavi-eligible countries: a modelling study,” Lancet Infect Dis, vol. 19, no. 1, pp. 102–111, Jan. 2019.
[57] A. Tarantola, S. Ly, M. Chan, S. In, Y. Peng, C. Hing, C. N. Taing, C. Phoen, S. Ly, S. Cauchemez, P. Buchy, P. Dussart, H. Bourhy, and J.-Y. Mary, “Intradermal rabies post-exposure prophylaxis can be abridged with no measurable impact on clinical outcome in Cambodia, 2003-2014.,” Vaccine, Nov. 2018.
[58] H. L. Beyer, K. Hampson, T. Lembo, S. Cleaveland, M. Kaare, and D. T. Haydon, “Metapopulation dynamics of rabies and the efficacy of vaccination,” Proceedings of the Royal Society B: Biological Sciences, vol. 278, no. 1715, pp. 2182–2190, Dec. 2010.
[59] N. Mollentze, L. H. Nel, S. Townsend, K. le Roux, K. Hampson, D. T. Haydon, and S. Soubeyrand, “A Bayesian approach for inferring the dynamics of partially observed endemic infectious diseases from space-time-genetic data.,” Proc. Biol. Sci., vol. 281, no. 1782, pp. 20133251–20133251, May 2014.
[60] A. Cori, P. Nouvellet, T. Garske, H. Bourhy, E. Nakouné, and T. Jombart, “A graph-based evidence synthesis approach to detecting outbreak clusters: An application to dog rabies,” PLoS Comput Biol, vol. 14, no. 12, pp. e1006554–22, Dec. 2018.
[61] S. E. Townsend, T. Lembo, S. Cleaveland, F. X. Meslin, M. E. Miranda, A. A. G. Putra, D. T. Haydon, and K. Hampson, “Surveillance guidelines for disease elimination: A case study of canine rabies,” “Comparative Immunology, Microbiology and Infectious Diseases,” vol. 36, no. 3, pp. 249–261, May 2013.
[62] J. Changalucha, R. Steenson, E. Grieve, S. Cleaveland, T. Lembo, K. Lushasi, G. Mchau, Z. Mtema, M. Sambo, A. Nanai, N. J. Govella, A. Dilip, L. Sikana, F. Ventura, and K. Hampson, “The need to improve access to rabies post-exposure vaccines: Lessons from Tanzania.,” Vaccine, Oct. 2018.
[63] K. Hampson, A. Dobson, M. Kaare, J. Dushoff, M. Magoto, E. Sindoya, and S. Cleaveland, “Rabies Exposures, Post-Exposure Prophylaxis and Deaths in a Region of Endemic Canine Rabies,” PLoS Negl Trop Dis, vol. 2, no. 11, pp. 1–9, Nov. 2008.
[64] K. Rysava, M. E. Miranda, R. Zapatos, S. Lapiz, P. Rances, L. M. Miranda, M. C. Roces, J. Friar, S. E. Townsend, and K. Hampson, “On the path to rabies elimination: The need for risk assessments to improve administration of post-exposure prophylaxis,” Vaccine, pp. 1–9, Dec. 2018.
[65] R. M. Wallace, H. Reses, R. Franka, P. Dilius, N. Fenelon, L. Orciari, M. Etheart, A. Destine, K. Crowdis, J. D. Blanton, C. Francisco, F. Ludder, V. Del Rio Vilas, J. Haim, and M. Millien, “Establishment of a Canine Rabies Burden in Haiti through the Implementation of a Novel Surveillance Program,” PLoS Negl Trop Dis, vol. 9, no. 11, pp. e0004245–15, Nov. 2015.
[66] M. Rajeev, G. Edosoa, C. Hanitriniaina, S. F. Andriamandimby, H. Guis, R. Ramiandrasoa, R. Ratovoson, L. Randrianasolo, M. Andriamananjara, J.-M. Heraud, L. Baril, C. J. E. Metcalf, and K. Hampson, “Healthcare utilization, provisioning of post-exposure prophylaxis, and estimation of human rabies burden in Madagascar,” Vaccine, pp. 1–10, Nov. 2018.
[67] “Rabies vaccines: WHO position paper,” WHO Wkly Epidemiol Rec, 2018.
[68] Tenzin, N. K. Dhand, and M. P. Ward, “Human rabies post exposure prophylaxis in Bhutan, 2005-2008: trends and risk factors.,” Vaccine, vol. 29, no. 24, pp. 4094–4101, May 2011.
[69] V. Duong, A. Tarantola, S. Ong, C. Mey, R. Choeung, S. Ly, H. Bourhy, P. Dussart, and P. Buchy, “Laboratory diagnostics in dog-mediated rabies: an overview of performance and a proposed strategy for various settings,” Int J Infect Dis, vol. 46, pp. 107–114, May 2016.
[70] L. Dacheux, J.-M. Reynes, P. Buchy, O. Sivuth, B. M. Diop, D. Rousset, C. Rathat, N. Jolly, J. B. Dufourcq, C. Nareth, S. Diop, C. Iehlé, R. Rajerison, C. Sadorge, and H. Bourhy, “A Reliable Diagnosis of Human Rabies Based on Analysis of Skin Biopsy Specimens,” Clinical Infectious Diseases, vol. 47, no. 11, pp. 1410–1417, Dec. 2008.
[71] D. Wentworth, K. Hampson, S. M. Thumbi, A. Mwatondo, G. Wambura, and N. R. Chng, “A social justice perspective on access to human rabies vaccines,” Vaccine, pp. 1–3, Apr. 2019.
[72] M. Léchenne, K. Naissengar, A. Lepelletier, I. O. Alfaroukh, H. Bourhy, J. Zinsstag, and L. Dacheux, “Validation of a Rapid Rabies Diagnostic Tool for Field Surveillance in Developing Countries,” PLoS Negl Trop Dis, vol. 10, no. 10, pp. e0005010–16, Oct. 2016.
[73] E. A. Undurraga, M. I. Meltzer, C. H. Tran, C. Y. Atkins, M. D. Etheart, M. F. Millien, P. Adrien, and R. M. Wallace, “Cost-Effectiveness Evaluation of a Novel Integrated Bite Case Management Program for the Control of Human Rabies, Haiti 2014–2015,” Am J Trop Med Hyg, vol. 96, no. 6, pp. 1307–1317, Jun. 2017.
[74] K. Brunker, P. Lemey, D. A. Marston, A. R. Fooks, A. Lugelo, C. Ngeleja, K. Hampson, and R. Biek, “Landscape attributes governing local transmission of an endemic zoonosis: Rabies virus in domestic dogs,” Molecular Ecology, vol. 27, no. 3, pp. 773–788, Feb. 2018.
[75] J. Zinsstag, M. Léchenne, M. Laager, R. Mindekem, S. Naïssengar, A. Oussiguere, K. Bidjeh, G. Rives, J. Tessier, S. Madjaninan, M. Ouagal, D. D. Moto, I. O. Alfaroukh, Y. Muthiani, A. Traoré, J. Hattendorf, A. Lepelletier, L. Kergoat, H. Bourhy, L. Dacheux, T. Stadler, and N. Chitnis, “Vaccination of dogs in an African city interrupts rabies transmission and reduces human exposure.,” Sci Transl Med, vol. 9, no. 421, p. eaaf6984, Dec. 2017.
[76] J. Hadfield, C. Megill, S. M. Bell, J. Huddleston, B. Potter, C. Callender, P. Sagulenko, T. Bedford, and R. A. Neher, “Nextstrain: real-time tracking of pathogen evolution | Bioinformatics | Oxford Academic,” Bioinformatics, vol. 34, no. 23, pp. 4121–4123, 2018.
[77] A. D. Gibson, P. Ohal, K. Shervell, I. G. Handel, B. M. Bronsvoort, R. J. Mellanby, and L. Gamble, “Vaccinate-assess-move method of mass canine rabies vaccination utilising mobile technology data collection in Ranchi, India,” BMC Infect. Dis., pp. 1–10, Dec. 2015.
[78] M. Sambo, P. C. D. Johnson, K. Hotopp, J. Changalucha, S. Cleaveland, R. Kazwala, T. Lembo, A. Lugelo, K. Lushasi, M. Maziku, E. Mbunda, Z. Mtema, L. Sikana, S. E. Townsend, and K. Hampson, “Comparing Methods of Assessing Dog Rabies Vaccination Coverage in Rural and Urban Communities in Tanzania,” Front Vet Sci, vol. 4, no. 8, pp. e0003709–12, Mar. 2017.
[79] T. Tenzin, J. S. McKenzie, R. Vanderstichel, B. D. Rai, K. Rinzin, Y. Tshering, R. Pem, C. Tshering, N. Dahal, K. Dukpa, S. Dorjee, S. Wangchuk, P. D. Jolly, R. Morris, and M. P. Ward, “Comparison of mark-resight methods to estimate abundance and rabies vaccination coverage of free-roaming dogs in two urban areas of south Bhutan.,” Preventive Veterinary Medicine, vol. 118, no. 4, pp. 436–448, Mar. 2015.
4.8 Supplementary Figures
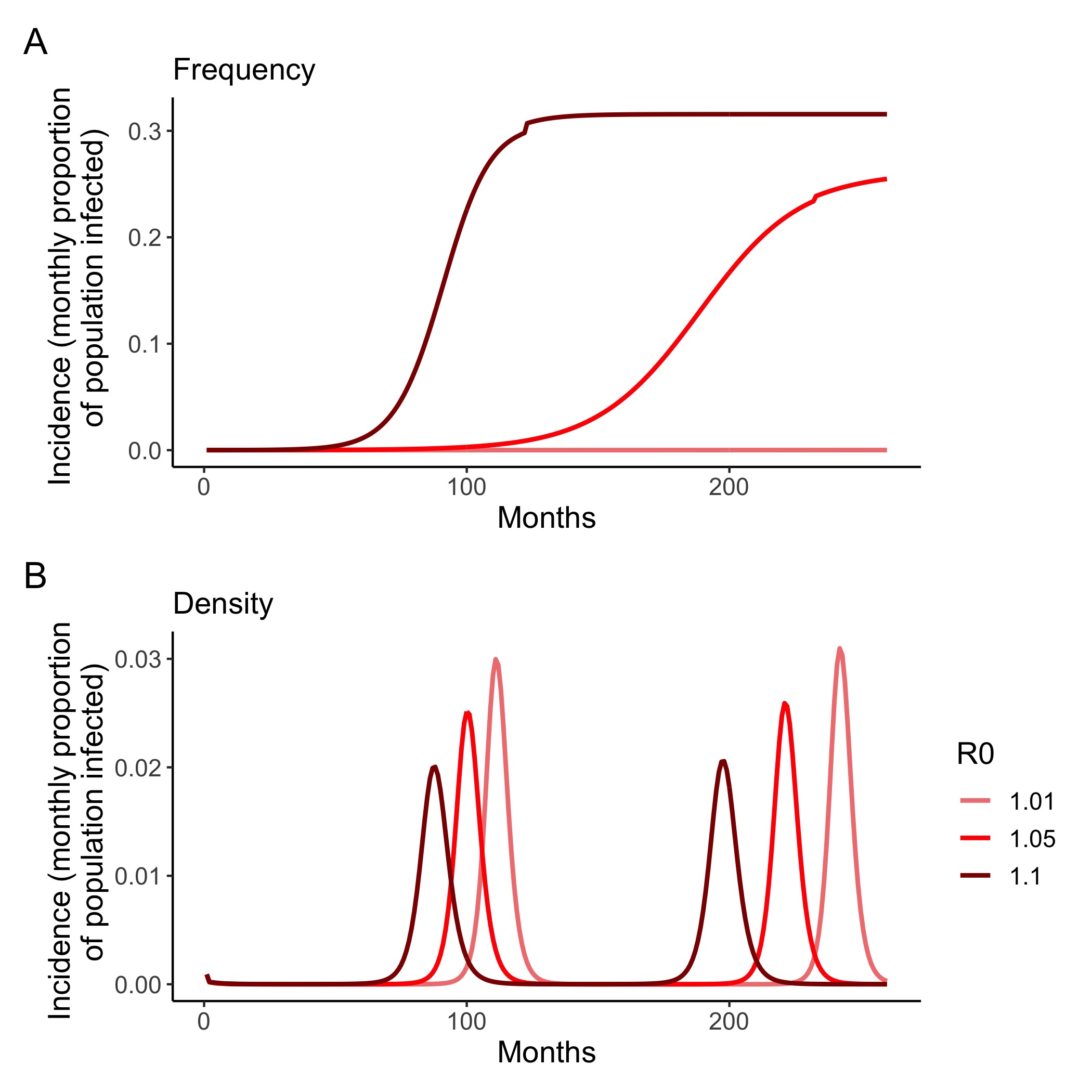
Figure 4.4: (ref:figS1-cap)
(ref:figS1-cap) Density vs. frequency-dependent transmission. Monthly incidence (the proportion of the population infected, and thus removed (as a result of mortality)) from mass-action models of rabies with A) frequency and B) density dependent transmission. Even in low transmission scenarios (R0 = 1.01 - 1.1), incidence peaks at between 1.5 – 2.0% per month for models with density-dependent transmission and between 0.01 - 30% for frequency-dependent transmission, compared with the 1 - 2% max annual incidence observed empirically. Demographic and transmission parameters are listed in Table 4.1 (mean incubation and infectious periods were input as annual rates). Frequency-dependent model is a SEI model with starting dog population of 50,000 and seeded with 2 infectious individuals. Density-dependent model is adapted from Anderson et al. 1981, with starting population density of 15 dogs per km2 , 0.01 infectious dogs per km2, and carrying capacity of 29 dogs per km2.
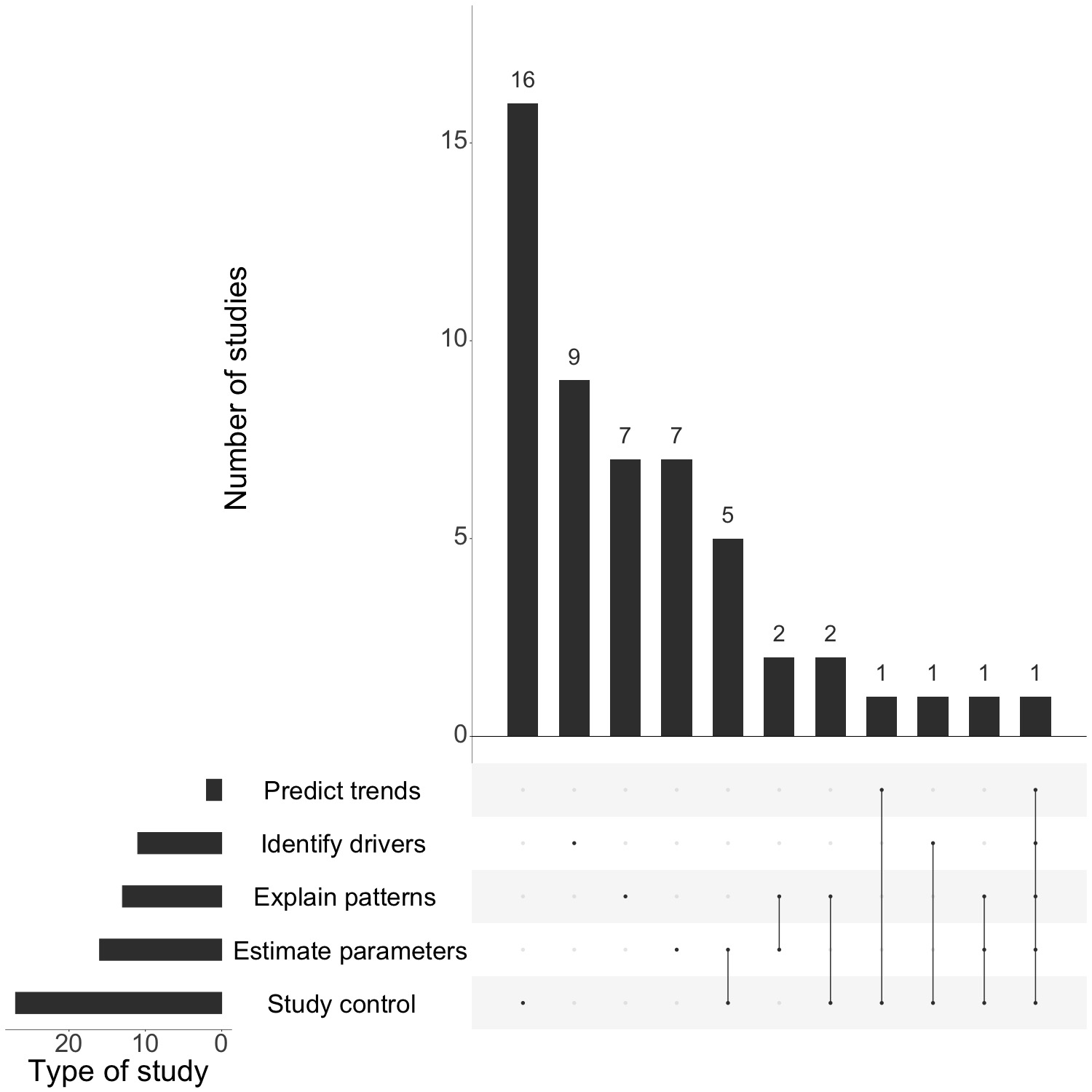
Figure 4.5: (ref:figS2-cap)
(ref:figS2-cap) Types of modeling studies. Categories areadapted from Lloyd-Smith et al. 2009: 1) Predict future trends based on currently available data and model projections; 2) Study control measures (using models to estimate/simulate the impacts of control efforts and compare intervention strategies); 3) Estimate key parameters such as Ro, the incubation period, the dispersal kernel; we also differentiate between studies which 4) Identify drivers of dynamics (that is look at hypothetical factors which may drive transmission without comparing or fitting to data) and studies which 5) Explain observed patterns (use models and data to determine likely drivers of observed patterns).